On Designing Mnemonic Systems – and Why Picture Notation is the Best Mnemonic Code for Chess
Memory palaces are a powerful tool to expand your memory. However, it’s not always obvious how to apply them. One of the common questions is, “I have [some complicated dataset]. How do I memorise it?”
I don’t claim to be an expert, but I have built quite a few memory palaces for exams, and in particular I have spent a long time pondering the best mnemonic system for chess. In this article I want to share where my thinking has reached, on the main points to consider when designing a mnemonic system.
This will also explain why I believe my book The Chess Memory Palace, with its mnemonic code of picture notation, is the best mnemonic system for chess, as mnemonists sometimes challenge the book on this point.
The essence of mnemonic systems is two steps: (1) work out the structure of your system of pegs, then (2) build a reliable code to convert non-memorable data into memorable data.
In this article, I have most to say about step 2. But we will begin with step 1, because sometimes the structure of the pegs will give you constraints in the way you can design the mnemonic code. Finally we will touch briefly on error detection and redundancy.
This is a relatively technical post. It will make most sense if you have some familiarity with the challenges of using mnemonics. My extended example of a mnemonic code (step 2) is picture notation for chess, so I recommend reading that first – but you should still be able to follow, even if you don’t know picture notation. (For simplicity, my chess examples will start from move 1, e.g. 1.e4 e5, but note that I don’t recommend you begin your chess memory palaces at move 1.)
Fundamentals of mnemonic theory
The rule of step 1 is: All mnemonics are about mapping something that you don’t know onto something that you do know. For example, you might not know the order of the planets, but you do know a series of landmarks in your street. You can then imagine the planets (or something that reminds you of the planets, e.g. a red warlike figure for Mars) in order along your street, creating visualisations (little stories) to associate one planet with one location, in order. (Do not get hung up on the word “visualisation” – people have different internal experiences, and even many people with aphantasia can build memory palaces. For most people, as long as you can remember stories and where they took place, it should be possible.)
The “things that you do know” structure the memories, so that you have a way of navigating through the entire dataset. In this case, you can mentally walk along your street from landmark to landmark, and recall the planet attached to each. The “things that you do know” are often called “pegs”. Traditionally they are locations, hence the names “memory palace”, “method of loci” or “journey method”, but they don’t have to be locations; they can be anything you know well, e.g. song lyrics, film scenes, football players in order of shirt number. (Joe Reddington in Advanced Memory Palaces notes the method of loci can be thought of as just “an array that is indexed by physical locations”, and the term is shorthand for “using physical locations a a source of keywords for an array”. Although, my vague understanding of the science is that there is something special about using locations rather than objects for pegs, as our brains remember the place where we learned something, and our neurons that store locations trigger slightly before we have the conscious knowledge of remembering the information.)
Non-linear memory palaces
Usually designing step 1, the system of pegs, is not too difficult. The vast majority of memory palaces I have read about are linear arrays, so you can use any linear journey of landmarks, film scenes, song lyrics etc.
How about tabular data (that has rows and columns)? One method is to use have a series of similarly-structured pegs (for the table rows) where you can attach the different data points (values, in the table columns) in a consistent way. For example, use five shops in a high street for five rows of data. Attach the data in column 1 to the doors, the data in column 2 to the windows. (This, alongside Karnaugh Maps (like Venn Diagrams) and binary trees, is discussed in Advanced Memory Palaces, and something similar for preparing to remember details about individuals in Moonwalking with Einstein.)
For chess, there is a challenge: chess openings take a branching tree structure (technically a directed graph when there are transpositions involved), so it is natural for the systems of pegs to also take a tree structure.
(As Joe Reddington pointed out to me in correspondence, the peg system for branching data doesn’t necessarily have to take a branching structure itself. An example would be, imagine you wanted to memorise an algorithm to win 21. You could memorise a big branching tree, or you could just memorise three pairs: “when my opponent says 1, I say 3”; “when my opponent says 2, I say 2”, “When my opponent says 3, I say 1”. This is obviously a toy example that doesn’t require a memory palace at all, but it shows the point that sometimes you can memorise a simple lookup table to navigate branching real-life data. This doesn’t work for chess, because move order matters, and you don’t always respond to the same move in the same way; it depends on the overall board position. Another approach would be to use computer science techniques to convert the branching data into a linear shape, but I haven’t yet found a satisfactory way to do this for an unbalanced tree like a chess opening.)
So how can we build a branching system of pegs? One correspondent on the Art of Memory Forum maps chess moves to branching family trees. This is ingenious but I think limited. It seems to me more versatile to use locations with branching paths. A figure from The Chess Memory Palace:
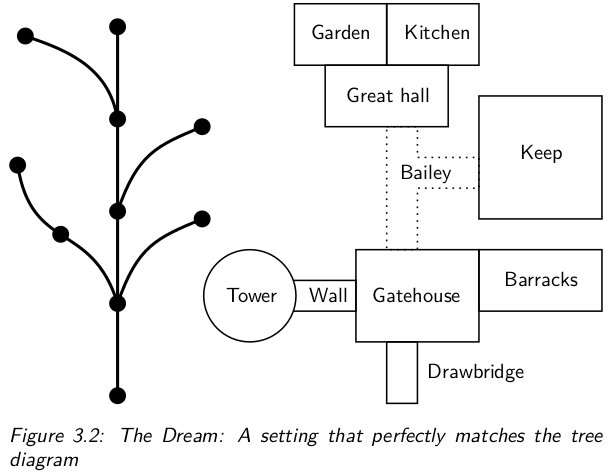
In my view this is actually a more natural way to use locations than a linear memory palace. In our experience of the world, most of our locational knowledge is as a network of places. For example, if I want to find a plate in my flat, I would enter the flat, go straight on to the kitchen, turn right to the cupboard. If I wanted to use the oven, I would enter the flat, go straight on to the kitchen, turn left to the oven. If I wanted to access the bookshelves, I would enter the flat, turn left to the living room, go to the far side of the room for the books, etc. My experience of my flat isn’t a linear journey hugging the edge of each room; it is more like a network of nodes. The same is true of my workplace, university campus, local town centre, etc.
In this way, you can use memory palaces to store branching data (or graphs with loops, or flowcharts). It does make less ‘efficient’ use of space than a linear memory palace, because you can’t fit too many locations in a room without the branching paths getting confused. But in practice I haven’t needed to worry about running out of settings. If you need more settings, you can always go and explore a new town, or play a new video game!
Whatever system of pegs you use, make sure you have a systematic method to walk through the entire thing (assuming your goal is to be able to reproduce all the information without external prompting). Despite what I have said above about trees, if possible I do think it is best to convert your data into a simple linear array. So, for example, never try to memorise an unordered set. Give it an order, even if the order is arbitrary.
Before we move to step 2 (the mnemonic code), we first we need to ask, does the design of pegs create any constraints on the mnemonic code? In the case of chess, the answer is yes. We want the memory palace to be able to branch after any pair of moves. Therefore each location (peg) can hold a maximum of one pair of moves.
Mnemonic codes
The rule of step 2 is: All mnemonics are about converting non-memorable data into memorable data. This means something that is easy to visualise, animate, and describe in stories: typically people and animals and emotive objects.
In the easiest cases, you don’t need a code at all, you can just visualise your target information directly. The classical example is memorising a shopping list. (I used to think this is a silly example because you can just write down a list, until one day my friend verbally gave me a list of ingredients to find while we entered a supermarket.) With a shopping list, you can just memorise the items themselves, with a bit of exagerration, such as eggs cracking, brocolli growing through the floor like trees, orange juice spilling over the shelves, etc.
In other cases, you can memorise one thing in place of another, but you don’t need a rigorous code. For example, for courage, imagine Mars or Achilles (The Dialexeis fragment, ~400 BC); for the Earl of Balfour, imagine a ‘ball 4’ pool ball (Ed Cooke), for Buchanan, imagine a cannon firing (my exam prep a few years ago).
The most difficult cases are truly abstract data, when you will need to design a rigorous code (and rote memorise it). The best known example is the major sytem for memorising numbers. The digits 0-9 are encoded onto consonent sounds, so that you can memorise words instead of numbers. For example, turtle bench lime encodes the first nine decimal places of pi (141592653). (I won’t explain the details here, it is easy to search.) Early versions of the major system date back to the 16th century. The practice of converting numerals to sounds for memorisation dates back at least as far as the Kaṭapayādi system in India, around 600 AD.
Memory world records have been slashed in the last 20 years. A lot of this has been due to the development of more efficient mnemonic codes. For example, using a version of the major system, you could memorise a deck of playing cards in 52 pictures (one picture per card). Ben Pridmore’s Ben system was revolutionary, as he created a way to memorise a pair of cards in a single picture, so now you can memorise a deck of cards in 26 pictures – at the cost of preparing pictures for 2704 possible combinations upfront. Another development noticed that you can use the pegs to encode information – e.g. use the same peg twice if the pair of cards starts with a red, move to a new peg if the pair of cards starts with a black. This halved the number of combinations to memorise upfront, to 1352.
A very popular mnemonic code for random digits is known as PAO: Person Action Object. In a 2-digit system, you would memorise 100 people, each with an action and an object. e.g. 15 might be Albert Einstein writing on a blackboard. 36 might be Michael Jackson moonwalking with a white glove. Then each set of 6 random digits can be converted into an image: e.g. 15-36-15 might be Albert Einstein moonwalking with a blackboard. (Hence the name of the most famous memory book, Moonwalking with Einstein.) In a 3-digit system, you would memorise 1000 people, each with an action and object. This is very powerful, as you can memorise 9 digits in a single composite image of 3 picture elements – but it carries the high upfront cost of preparing and memorising pictures of 1000 people, actions and objects. (Some people use 1000 people and objects but only 100 actions, to code 8 digits at a time.)
Mnemonic code for chess moves: the specifications
How does this apply to chess? The first thing to note is that fewer images is better. If you can memorise 9 digits in a single composite image, that’s more efficient than memorising 6 digits in a composite image. For chess, we have seen from the peg structure that we want to memorise a maximum of one pair of moves (e.g. e4 e5) in a single image, because the palace may need to branch after any pair of moves. So, ideally, we want to memorise this in a single image, or one image for each of the half-moves.
The second thing to note is that memory competitors need to do lots of work to memorise their images upfront, because they need to convert data to pictures in their heads. For example, when they see 15, they need to immediately know that is coded as Albert Einstein, so that they can quickly memorise it under memory tournament conditions. (In other words, they need their mnemonic system to be ‘bidirectional’ (Anthony Metivier).) In chess this is different: we can memorise our opening repertoires at leisure at home. I don’t need to convert e.g. Nf3 from a chess move into a mnemonic picture in my head: I can just look up the code in the appendix. All I need to do at the board is convert a mnemonic picture back into a chess move. So, we need a system that is easy to convert a picture to a chess move, but it does not need to be easy to convert a chess move into a picture in our heads. So, we don’t need to make compromises in order to minimise the number of picture words in the system.
Third, and this is very important (although I began to understand it more fully only after I had published), memory competitors are memorising uniformly distributed random data. Each of their image combinations will come up with roughly equal frequency. “PAO works at its best when the information to memorise is uniformly distributed. i.e. 100 rolls of a single dice. When the same Ps, As, or Os turn up a lot, you get very likely to make mistakes (‘Einstein is moonwalking with a banana, now Einstein is moonwalking with a Lego, now Trump is moonwalking with a banana’) […] In general, I’d go as far as to say that PAO is a poor choice for any structured data” (Joe Reddington) (It would be interesting to see a memory competition where the random digits are not uniformly distributed, but were heavily weighted towards certain digits – would competitors need to adapt their techniques?) With chess openings, the data is not at all randomly or uniformly distributed. There are many more moves to the central squares than the squares round the edge of the board. So, we want a system where we have sufficient variation in the pictures we use, despite the same target squares turning up repeatedly.
How picture notation meets these specifications, and why PAO and alternatives do not
Picture notation codes every chess move (except for obscure things like underpromotions) in a single picture word. For example, in the starting position, shampoo means 1.f3, because the sh and m code the f3 square, and the number of syllables (2) codes the second candidate pieces (the pawn – the knight would have been the first candidate piece, because it’s on the back rank). This means any pair of moves can be shown in a single composite image of two picture words, e.g. “shampoo pouring over a judge” could be 1.f3 Nf6.
This is, I think, the most efficient way to encode a pair of moves. The most obvious solution is to encode both the starting and target square of each move, e.g. 1.f3 Nf6 becomes 6263 7866 (i.e. International Correspondence Chess Federation numeric notation). But memorising the starting square is overkill; there is usually a maximum of four candidate pieces that can move to the target square, so you only need to identify it on a scale of 1-4, not the 1-64 squares of the chessboard.
The second obvious solution is to use algebraic notation, e.g. memorise that the piece to move is a knight or a pawn. The problem with this is the edge cases where two of the same piece can move to the same square. You’d need another system to deal with these tiebreaks. This can be done using the digits 1-9 (king, queen, left rook, right rook, bishop, left knight, right knight, left pawn, right pawn) – but this is more than double picture notation’s candidate piece scale (thus limiting the picture words you can use) and undermines the purpose of using the ‘more intuitive’ algebraic notation as the basis of the mnemonic code.
The third obvious solution is not to bother memorising the piece that moves. This is the most common solution I have seen proposed online. e.g. if you memorise the target squares e4 e5 f3 c6, any chess player will recognise that the moves are 1.e4 e5 2.Nf3 Nc6. I have seen this justified as “you don’t need to memorise which piece moves” (not quoting anyone in particular). The drawback of this, of course, is that it leaves ambiguities. The piece to move isn’t always obvious. And the justification is a misunderstanding. If you had to memorise a more complicated image in order to memorise the candidate piece, I would agree it might be worth the compromise of not memorising the candidate piece. But, we are not trying to minimise the total information memorised. We are trying to minimise the total number of images (and elements within the images). Picture notation uses the number of syllables within the picture word to identify the candidate piece, so it does not increase the number of images to memorise. Identifying the candidate piece with syllables is costless. (Costless in terms of memory space. There is a slight cost in reducing your set of available picture words to choose from. But there are still lots of options.)
Mnemonists naturally want to apply PAO. This hides a couple of difficulties. First, how exactly PAO, a digit system, will unambiguously code chess moves. It is possible to use PAO to code a pair of chess moves – but to my mind, this is 50% worse than using picture notation, because picture notation needs only two elements in each composite image, not three. (This also means that picture notation can easily be decoded (from image to chess move) one half-move at a time, which is simpler at the board than decoding both P and A, then A and O, to recover the two half-moves.) Second, because of the non-random nature of chess moves, you will end up with lots of the same Ps, As and Os, which is hard to memorise. Picture notation solves this problem in two ways: (1) each square can take several picture words, depending on the candidate piece. e.g. d4 will somtimes be roar, sometimes robber, and occasionally warrior or barbarian. (2) If you are seeing one picture word too often, you can always substitute an equivalent, e.g. briar or wrapper instead of robber.
Another suggestion I have seen in correspondence is to just have 64 base images, and transform the images to indicate the candidate piece. e.g. a pearl is d5 with the first candidate piece, a pearl on fire is d5 with the second candidate piece, a pearl covered in oil is d5 with the third candidate piece, etc. This works in theory, in fact I suggest it in the section on Picture notation in other languages in Chapter 7 – but only if there is no other solution, such as syllables, tone sounds, or grammatical gender. This system needs four elements in each composite image instead of two – with correspondingly more interactions – and also runs into the problem of trying to memorise lots of similar images. Remember, we can build our memory palaces at home with full use of the appendix, so there is no fixed cost of memorising all the picture words upfront, unlike memory competitors memorising digits and decks of cards.
The final advantage of picture notation is that it is easy to share with others, unlike PAO. But this isn’t the reason I designed it this way.
There are probably lots of ways to design a mnemonic code for chess that keeps 1 picture = 1 half-move, so it is possible to come up with systems that are equally as good as picture notation – but for all the reasons set out in this blog post, I don’t think it is possible to make a system that is better. One alternative is to count letters rather than syllables, but this requires you to spell words accurately in your head, which is harder. The only way I can think of to improve picture notation would be to code two half-moves in a single picture – but this would require six items of information in a single picture (two target files, two target ranks, two candidate pieces), which I don’t believe will be possible. It’s also not necessarily an improvement, because at the board it can be easier to decode one half-move at at time. (An exception might be to create some images for common move-pairs. For example, roar roar is fairly common; you could systematically replace this with a new single image.)
A word on error detection and redundancy
Finally, a note on error detection and correction. Some mnemonists, when memorising data for the medium to long term, will overlap some of their images, so that some digits are memorised twice (e.g. Nelson Dellis). This helps catch errors, and offers a hint if they remember one image but not the next. (You could also come up with checksums if you are able or don’t need to do the calculations in your head. If I ever memorise something critical, I will definitely include lots of extra error correction images, or just memorise the whole thing twice with different pictures. One of the interesting but rarely applicable properties of mnemonics, compared with rote-learning raw facts, is that it makes “memorise it twice” possible as a concept.)
Similarly, one piece of advice recommended since ancient times is to have a door or window every five or ten locations along your memory palace. This is excellent advice if you are designing a traditional linear memory palace, as it chunks your memories into digestible groups of five, and acts as a safety mechanism to alert you if you forget a location. Both techniques can be useful, but are unnecessary for chess, because the board position itself will validate or invalidate your moves. (I discuss several reasons why The Chess Memory Palace doesn’t use the doors and windows idea in Note 5 to Chapter 3.)
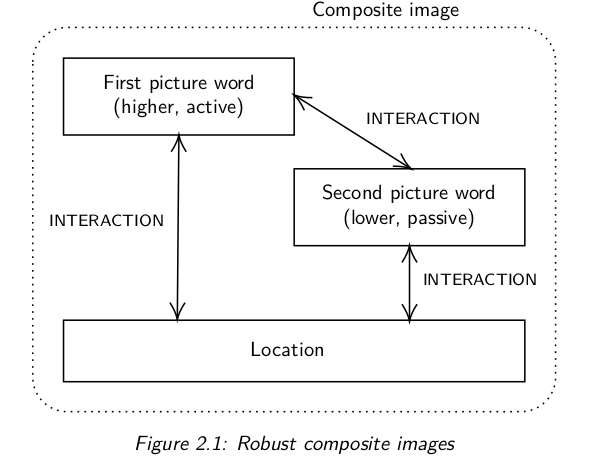
The diagram above hasn’t attracted any comment, but it is my favourite diagram in the book. The ideas are not new; they are based on techniques memory competitors use to store two pictures together in a location without getting the order confused. But formalising it like this helped me memorise images more consistently. The point I want to emphasise here is that I recommend visualising all three interactions, not just two, and that we have dual indicators of picture word order: active versus passive roles and higher versus lower position. These are forms of redundancy (another term I picked up from Advanced Memory Palaces).
In theory, you would only need to visualise two of the three interactions to be able to recover both picture words, and in theory you only need a single rule to remind you which picture word is first and which is second. But this makes your memory less robust: if you have any lapse in memory, the information is lost. By having redundancy, you should still be able to recover 100% of the information, even if you start to forget details, e.g. you forget one of the three interactions, or you remember which picture word is higher but forget which is doing the action to the other.
When designing rules to store data in a memory palace, there is a trade-off between writing strict rules with added redundancy, versus leaving room for creative images. There is also a trade-off between spending time visualising detailed images in the first place, versus spending time reviewing and rebuilding broken links later. In general, the more you want to memorise, and the longer the time period over which you want to retain the memories, the more you should come down on the first side of both of these trade-offs. The Chess Memory Palace method needs to work for large quantities of chess moves over a long playing career, hence I advise detailed images and lots of redundancy.
When designing your own mnemonic systems, consider where you want to land on these trade-offs. Do you want special markers every five/ten pegs, strict rules for the images, and memorise extra images for error detection/correction, or is it not worth it?
Analysis paralysis
Having written a 4000 word essay, it’s still important to not overthink it. Sometimes you just need to start, and you will work out the problems as you go along. My early versions of picture notation used picture transformations, vowel sounds and a complicated piece-priority system to choose the candidate piece. I only simplified it over time, and particularly when writing the book, as explaining a system forces you to iron out any unnecessary complications. (This also meant that I had a bunch of old chess memory palaces in my mind that used outdated technology, which I have gradually let decay, apart from a few annoyingly persistent images. This is how I can say with confidence that “your best images will remain with you effortlessly for a decade” (page 145)).
So, it’s worth designing the best system you can upfront, and I hope this blog post will be helpful in that endeavour. But don’t get too bogged down: the best system is the system you will actually use.